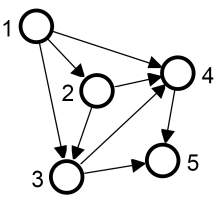
|
|
|
|
Target graph
|
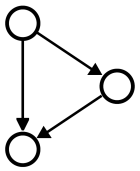
Motif
|
Matches of the motif in the target graph
Three concepts are considered for the determination of motif frequency, which have different applications and restrictions on counting overlapping matches (i.e. matches sharing edges or vertices) for motif frequency. Concepts F1 has no restrictions, concept F2 allows the sharing of vertices but not of edges and concept F3 does not allow any sharing of network elements. For concept F1 the frequency is given by the number of all matches. The restrictions on the reuse of graph elements for concepts F2 and F3 have consequences for the determination of motif frequency in case of overlapping matches, as not all matches can be counted for the frequency. To determine the maximum number of different matches of a motif the maximum set of non-overlapping matches has to be calculated. This is known as the maximum independent set problem. Since this problem is NP-complete, usually a heuristic is used to compute a lower bound for the frequency.
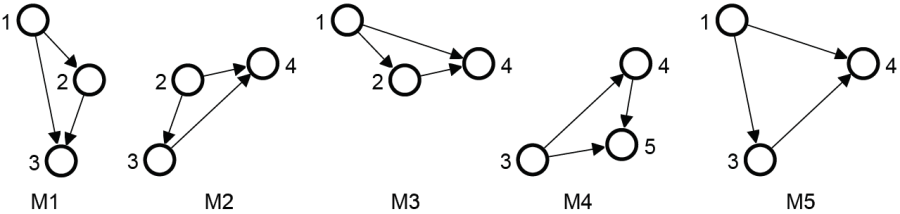
The table below summarizes the properties of the frequency concepts and lists the values for the presented example:
| Frequency Concept | Frequency Determination | Shared Elements | Values for the example below | ||
|---|---|---|---|---|---|
| Vertices | Edges | Frequency | Selected matches | ||
| F1 | All Matches | + | + | 5 | {M1,M2,M3,M4,M5} |
| F2 | Maximum Independet Set | + | - | 2 | {M1,M4} or {M3,M4} |
| F3 | Maximum Independet Set | - | - | 1 | one of {M1,M2,M3,M4,M5} |
|
||||||
|
|
||||||
|
Matches of the motif in the target graph
|
| Contact |
|